
你好,我是黄申。今天我们来聊聊“余数”。
提起来余数,我想你肯定不陌生,因为我们生活中就有很多很多与余数相关的例子。
比如说,今天是星期三,你想知道50天之后是星期几,那你可以这样算,拿50除以7(因为一个星期有7天),然后余1,最后在今天的基础上加一天,这样你就能知道50天之后是星期四了。
再比如,我们做Web编程的时候,经常要用到分页的概念。如果你要展示1123条数据,每页10条,那该怎么计算总共的页数呢?我想你肯定是拿1123除以10,最后得到商是112,余数是3,所以你的总页数就是112+1=113,而最后的余数就是多出来,凑不够一页的数据。
看完这几个例子,不知道你有没有发现,余数总是在一个固定的范围内。
比如你拿任何一个整数除以7,那得到的余数肯定是在0~6之间的某一个数。所以当我们知道1900年的1月1日是星期一,那便可以知道这一天之后的第1万天、10万天是星期几,是不是很神奇?
你知道,整数是没有边界的,它可能是正无穷,也可能是负无穷。但是余数却可以通过某一种关系,让整数处于一个确定的边界内。我想这也是人类发明星期或者礼拜的初衷吧,任你时光变迁,我都是以7天为一个周期,“周”而复始地过着确定的生活。因为从星期的角度看,不管你是哪一天,都会落到星期一到星期日的某一天里。
我们再拿上面星期的例子来看。假如今天是星期一,从今天开始的100天里,都有多少个星期呢?你拿100除以7,得到商14余2,也就是说这100天里有14周多2天。换个角度看,我们可以说,这100天里,你的第1天、第8天、第15天等等,在余数的世界里都被认为是同一天,因为它们的余数都是1,都是星期一,你要上班的日子。同理,第2天、第9天、第16天余数都是2,它们都是星期二。
这些数的余数都是一样的,所以被归类到了一起,有意思吧?是的,我们的前人早已注意到了这一规律或者特点,所以他们把这一结论称为同余定理。简单来说,就是两个整数a和b,如果它们除以正整数m得到的余数相等,我们就可以说a和b对于模m同余。
也就是说,上面我们说的100天里,所有星期一的这些天都是同余的,所有星期二的这些天就是同余的,同理,星期三、星期四等等这些天也都是同余的。
还有,我们经常提到的奇数和偶数,其实也是同余定理的一个应用。当然,这个应用里,它的模就是2了,2除以2余0,所以它是偶数;3除以2余1,所以它是奇数。2和4除以2的余数都是0,所以它们都是一类,都是偶数。3和5除以2的余数都是1,所以它们都是一类,都是奇数。
你肯定会说,同余定理就这么简单吗,这个定理到底有什么实际的用途啊?其实,我上面已经告诉你答案了,你不妨先自己思考下,同余定理的意义到底是什么。
简单来说,同余定理其实就是用来分类的。你知道,我们有无穷多个整数,那怎么能够全面、多维度地管理这些整数?同余定理就提供了一个思路。
因为不管你的模是几,最终得到的余数肯定都在一个范围内。比如我们上面除以7,就得到了星期几;我们除以2,就得到了奇偶数。所以按照这种方式, 我们就可以把无穷多个整数分成有限多个类。
这一点,在我们的计算机中,可是有大用途。
哈希(Hash)你应该不陌生,在每个编程语言中,都会有对应的哈希函数。哈希有的时候也会被翻译为散列,简单来说,它就是将任意长度的输入,通过哈希算法,压缩为某一固定长度的输出。这话听着是不是有点耳熟?我们上面的求余过程不就是在做这事儿吗?
举个例子,假如你想要快速读写100万条数据记录,要达到高速地存取,最理想的情况当然是开辟一个连续的空间存放这些数据,这样就可以减少寻址的时间。但是由于条件的限制,我们并没有能够容纳100万条记录的连续地址空间,这个时候该怎么办呢?
我们可以考察一下,看看系统是否可以提供若干个较小的连续空间,而每个空间又能存放一定数量的记录。比如我们找到了100个较小的连续空间,也就是说,这些空间彼此之间是被分隔开来的,但是内部是连续的,并足以容纳1万条记录连续存放,那么我们就可以使用余数和同余定理来设计一个散列函数,并实现哈希表的结构。
那这个函数应该怎么设计呢?你可以先停下来思考思考,提醒你下,你可以再想想星期几的那个例子,因为这里面用的就是余数的思想。

下面是我想到的一种方法:
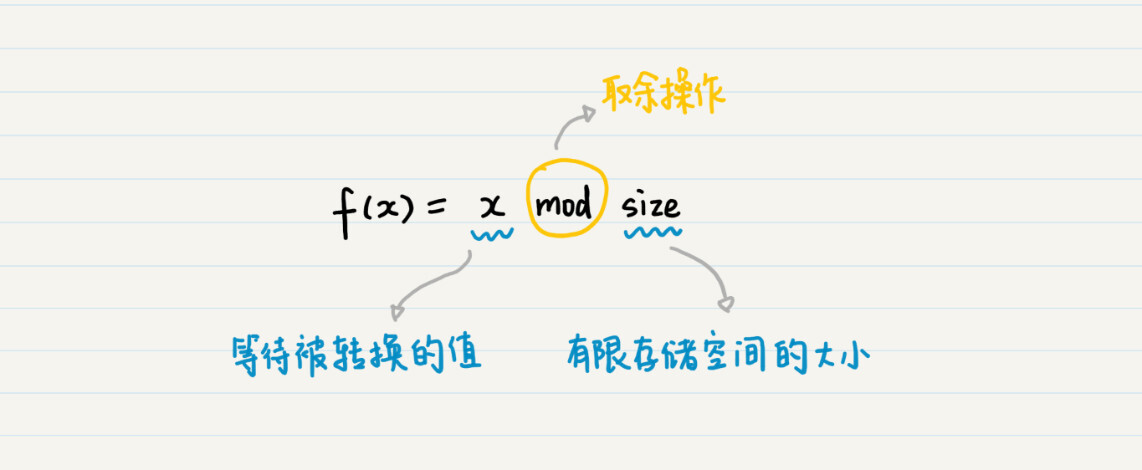
在这个公式中,x表示等待被转换的数值,而size表示有限存储空间的大小,mod表示取余操作。通过余数,你就能将任何数值,转换为有限范围内的一个数值,然后根据这个新的数值,来确定将数据存放在何处。
具体来说,我们可以通过记录标号模100的余数,指定某条记录存放在哪个空间。这个时候,我们的公式就变成了这样:

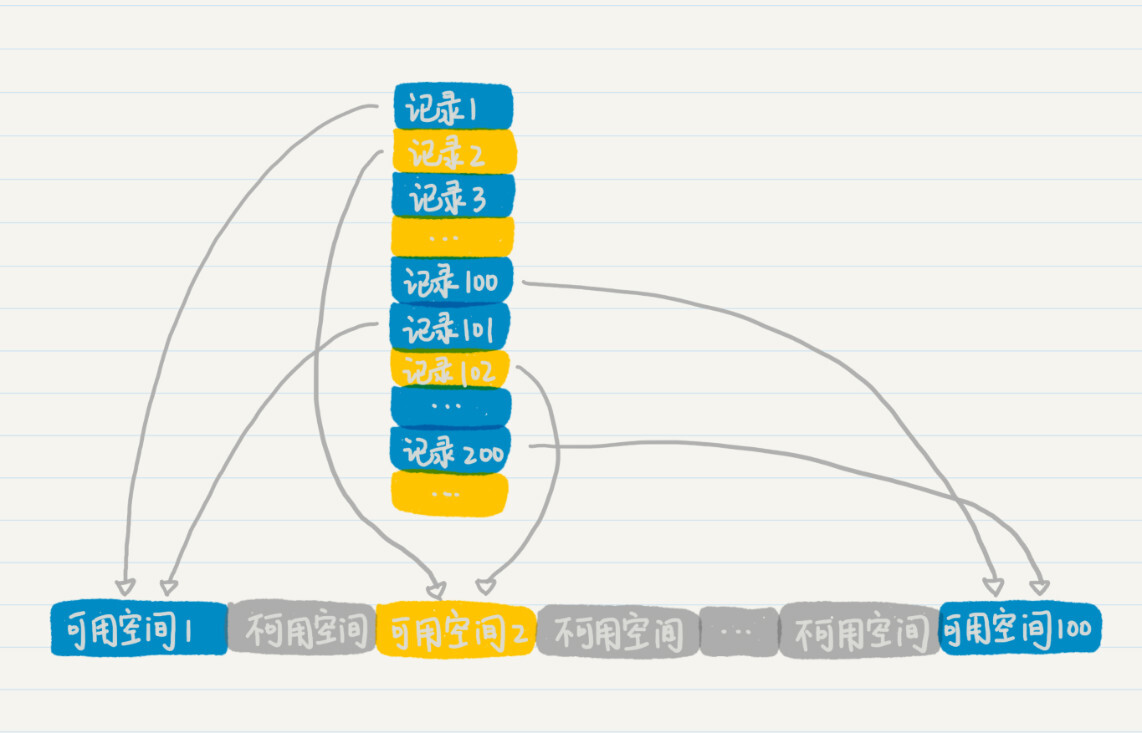
假设有两条记录,它们的记录标号分别是1和101。我们把这些模100之后余数都是1的,存放到第1个可用空间里。以此类推,将余数为2的2、102、202等,存放到第2个可用空间,将100、200、300等存放到第100个可用空间里。
这样,我们就可以根据求余的快速数字变化,对数据进行分组,并把它们存放到不同的地址空间里。而求余操作本身非常简单,因此几乎不会增加寻址时间。
除此之外,为了增加数据散列的随机程度,我们还可以在公式中加入一个较大的随机数MAX,于是,上面的公式就可以写成这样:

我们假设随机数MAX是590199,那么我们针对标号为1的记录进行重新计算,最后的计算结果就是0,而针对标号101的记录,如果随机数MAX取627901,对应的结果应该是2。这样先前被分配到空间1的两条记录,在新的计算公式作用下,就会被分配到不同的可用空间中。
你可以尝试记录2和102,或者记录100和200,最后应该也是同样的情况。你会发现,使用了MAX这个随机数之后,被分配到同一个空间中的记录就更加“随机”,更适合需要将数据重新洗牌的应用场景,比如加密算法、MapReduce中的数据分发、记录的高速查询和定位等等。
让我以加密算法为例,在这里面引入MAX随机数就可以增强加密算法的保密程度,是不是很厉害?举个例子,比如说我们要加密一组三位数,那我们设定一个这样的加密规则:
-
先对每个三位数的个、十和百位数,都加上一个较大的随机数。
-
然后将每位上的数都除以7,用所得的余数代替原有的个、十、百位数;
-
最后将第一位和第三位交换。
这就是一个基本的加密变换过程。
假如说,我们要加密数字625,根据刚才的规则,我们来试试。假设随机数我选择590127。那百、十和个位分别加上这个随机数,就变成了590133,590129,590132。然后,三位分别除以7求余后得到5,1,4。最终,我们可以得到加密后的数字就是415。因为加密的人知道加密的规则、求余所用的除数7、除法的商、以及所引入的随机数590127,所以当拿到415的时候,加密者就可以算出原始的数据是625。是不是很有意思?
小结
到这里,余数的所有知识点我们都讲完了。我想在此之前,你肯定是知道余数,也明白怎么求余。但对于余数的应用不知道你之前是否有思考过呢?我们经常说,数学是计算机的基础,在余数这个小知识点里,我们就能找到很多的应用场景,比如我前面介绍的散列函数、加密算法,当然,也还有我们没有介绍到的,比如循环冗余校验等等。
余数只是数学知识中的沧海一粟。你在中学或者大学的时候,肯定接触过很多的数学知识和定理,编程的时候也会经常和数字、公式以及数据打交道,但是真正学懂数学的人却没几个。希望我们可以从余数这个小概念开始,让你认识到数学思想其实非常实用,用好这些知识,对你的编程,甚至生活都有意想不到的作用。

思考题
你可以想想,在生活和编程中,还有哪些地方用到了余数的思想呢?
欢迎在留言区交作业,并写下你今天的学习笔记。你可以点击“请朋友读”,把今天的内容分享给你的好友,和他一起精进。

精选留言
"假如说,我们要加密数字 625,根据刚才的规则,我们来试试。假设随机数我选择 590127。那百、十和个位分别加上这个随机数,就变成了 590133,590129,590132。然后,三位分别除以 7 求余后得到 5,1,4。最终,我们可以得到加密后的数字就是 415。因为加密的人知道加密的规则、求余所用的除数 7、除法的商、以及所引入的随机数 590127,所以当拿到 415 的时候,加密者就可以算出原始的数据是 625。是不是很有意思?"
正向加密可以理解.
反向解密感觉有点问题呀.
--------------
625中间的数字2: (2 + 590127)%7 = 1. 但是(9 + 590127)%7 = 1
--------------
那么625和695最终加密后的结果都是415啊.
那就不一定能还原出来原始的值了啊.
--------------
另外,如果最后一位数字加密后的结果是0, 交换位置后, 会有麻烦吧.
System.out.println("加密前:" + num);
// 1.取余 并 加上随机数
int bit = num % 10;
int tenBit = num % 100 / 10;
int hundredBit = num % 1000 / 100;
System.out.println(bit + "\t" + tenBit + "\t" + hundredBit);
bit = bit + MAX;
tenBit = tenBit + MAX;
hundredBit = hundredBit + MAX;
System.out.println(bit + "\t" + tenBit + "\t" + hundredBit);
// 2.每个位数 除以7 取余代替原来的个十百
bit = bit % MULTIPLE;
tenBit = tenBit % MULTIPLE;
hundredBit = hundredBit % MULTIPLE;
System.out.println(bit + "\t" + tenBit + "\t" + hundredBit);
// 3.swap 第一位和第三位
int temp;
temp = bit;
bit = hundredBit;
hundredBit = temp;
System.out.println(bit + "\t" + tenBit + "\t" + hundredBit);
int result = bit + tenBit * 10 + hundredBit * 100;
System.out.println("加密结果为:" + result);
return result;
}
public static int decryptNum(int num) {
System.out.println("解密前:" + num);
// 1.取余
int bit = num % 10;
int tenBit = num % 100 / 10;
int hundredBit = num % 1000 / 100;
// 2.交互位数
int temp;
temp = bit;
bit = hundredBit;
hundredBit = temp;
// 3.乘回7的倍数
// 这里可能有bug 只能针对当前的MAX值 如果换了一个随机值 要考虑 是否要+1
int temp2 = (MAX / MULTIPLE) + 1;
bit = bit + temp2 * MULTIPLE;
tenBit = tenBit + temp2 * MULTIPLE;
hundredBit = hundredBit + temp2 * MULTIPLE;
// 4.减去随机数
bit = bit - MAX;
tenBit = tenBit - MAX;
hundredBit = hundredBit - MAX;
System.out.println(bit + "\t" + tenBit + "\t" + hundredBit);
int result = bit + tenBit * 10 + hundredBit * 100;
System.out.println("解密结果为:" + result);
return result;
}
num = 7
def encode_number(number):
rs = []
for i in number:
t = (int(i) + rand_max) % num
rs.append(t)
print(''.join([str(x) for x in rs]))
但是解密的过程就有点玄乎了,因为0-9的数字在对7进行取余的时候会有同样的结果出来,这个时候要补充商才比较合适一点。
除法是被除数除以除数,结果包含商和余数,记做:a/b
只求余数的除法,叫取模。记做 a%b
应用举例:
取模运算的特点,无论a多大,只要b固定,那么a%b的余数总是在一个有限范围内。这种特点相当于将a进行了降维和分类,跟方便我们认知世界。
比如今天是星期一,10000天后是星期几。就可以通过求余数来计算。因为今天是星期一,所以相对于今天的7天后,肯定也是星期一。
那1w天中,7的整数倍日期,肯定也都是星期一,唯一要看的,就是最终余数多少,那就相当于距离星期一几天。所以1w天后是星期几变成了
公式:(星期一 + 1w%7) 由于1w%7 = 4 ,说明是星期一的四天后,于是相对于今天1w天后是星期五
取模增加随机性:
连续的整数,在取模时,其余数也是周期连续的。比如:10%7 = 3 , 11%7=4 。余数算作一分钟分类,某些情况下,我们不希望原始数据的连续性,
在分类后也连续。为了增加几个班同学之间随机组合,增加交流。比如你不希望一个班(他们的学号相同),被分配到连续的组里。
那可以在取模之间,对原始数据做一些规则转换,让连续的原始数据变得不连续。比如给原始数据加一个随机数。
公式为:(a + random) % b
注意在一次分类活动中,random是固定的,不是每个数来都重新来个random。random就相当于hash算的中的hash因子。
当然为了使得原始连续数据不连续还有其他很多种方式,比如数据的不同位树互换等等。
文章谬误:
文章中所说的加密算法,再缺乏商时,无法完成解密,因为数据被降维了。