
你好,我是黄申。
上一节,我解释了如何使用递归,来处理迭代法中比较复杂的数值计算。说到这里,你可能会问了,有些迭代法并不是简单的数值计算,而要通过迭代的过程进行一定的操作,过程更加复杂,需要考虑很多中间数据的匹配或者保存。例如我们之前介绍的用二分查找进行数据匹配,或者我们今天将要介绍的归并排序中的数据排序等等。那么,这种情况下,还可以用递归吗?具体又该如何来实现呢?
我们可以先分析一下,这些看似很复杂的问题,是否可以简化为某些更小的、更简单的子问题来解决,这是一般思路。如果可以,那就意味着我们仍然可以使用递归的核心思想,将复杂的问题逐步简化成最基本的情况来求解。因此,今天我会从归并排序开始,延伸到多台机器的并行处理,详细讲讲递归思想在“分而治之”这个领域的应用。
归并排序中的分治思想
首先,我们来看,如何使用递归编程解决数字的排序问题。
对一堆杂乱无序的数字,按照从小到大或者从大到小的规则进行排序,这是计算机领域非常经典,也非常流行的问题。小到Excel电子表格,大到搜索引擎,都需要对一堆数字进行排序。因此,计算机领域的前辈们研究排序问题已经很多年了,也提出了许多优秀的算法,比如归并排序、快速排序、堆排序等等。其中,归并排序和快速排序都很好地体现了分治的思想,今天我来说说其中之一的归并排序(merge sort)。
很明显,归并排序算法的核心就是“归并”,也就是把两个有序的数列合并起来,形成一个更大的有序数列。
假设我们需要按照从小到大的顺序,合并两个有序数列A和B。这里我们需要开辟一个新的存储空间C,用于保存合并后的结果。
我们首先比较两个数列的第一个数,如果A数列的第一个数小于B数列的第一个数,那么就先取出A数列的第一个数放入C,并把这个数从A数列里删除。如果是B的第一个数更小,那么就先取出B数列的第一个数放入C,并把它从B数列里删除。
以此类推,直到A和B里所有的数都被取出来并放入C。如果到某一步,A或B数列为空,那直接将另一个数列的数据依次取出放入C就可以了。这种操作,可以保证两个有序的数列A和B合并到C之后,C数列仍然是有序的。
为了你能更好地理解,我举个例子说明一下,这是合并有序数组{1, 2, 5, 8}和{3, 4, 6}的过程。

为了保证得到有序的C数列,我们必须保证参与合并的A和B也是有序的。可是,等待排序的数组一开始都是乱序的,如果无法保证这点,那归并又有什么意义呢?
还记得上一篇说的递归吗?这里我们就可以利用递归的思想,把问题不断简化,也就是把数列不断简化,一直简化到只剩1个数。1个数本身就是有序的,对吧?
好了,现在剩下的疑惑就是,每一次如何简化问题呢?最简单的想法是,我们把将长度为n的数列,每次简化为长度为n-1的数列,直至长度为1。不过,这样的处理没有并行性,要进行n-1次的归并操作,效率就会很低。

所以,我们可以在归并排序中引入了分而治之(Divide and Conquer)的思想。分而治之,我们通常简称为分治。它的思想就是,将一个复杂的问题,分解成两个甚至多个规模相同或类似的子问题,然后对这些子问题再进一步细分,直到最后的子问题变得很简单,很容易就能被求解出来,这样这个复杂的问题就求解出来了。
归并排序通过分治的思想,把长度为n的数列,每次简化为两个长度为n/2的数列。这更有利于计算机的并行处理,只需要log2n次归并。

我们把归并和分治的思想结合起来,这其实就是归并排序算法。这种算法每次把数列进行二等分,直到唯一的数字,也就是最基本的有序数列。然后从这些最基本的有序数列开始,两两合并有序的数列,直到所有的数字都参与了归并排序。
我用一个包含0~9这10个数字的数组,给你详细讲解一下归并排序的过程。
-
假设初始的数组为{7, 6, 2, 4, 1, 9, 3, 8, 0, 5},我们要对它进行从小到大的排序。
-
第一次分解后,变成两个数组{7, 6, 2, 4, 1}和{9, 3, 8, 0, 5}。
-
然后,我们将{7, 6, 2, 4, 1}分解为{7, 6}和{2, 4, 1},将{9, 3, 8, 0, 5}分解为{9, 3}和{8, 0, 5}。
-
如果细分后的组仍然多于一个数字,我们就重复上述分解的步骤,直到每个组只包含一个数字。到这里,这些其实都是递归的嵌套调用过程。
-
然后,我们要开始进行合并了。我们可以将{4, 1}分解为{4}和{1}。现在无法再细分了,我们开始合并。在合并的过程中进行排序,所以合并的结果为{1,4}。合并后的结果将返回当前函数的调用者,这就是函数返回的过程。
-
重复上述合并的过程,直到完成整个数组的排序,得到{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}。
为了方便你的理解,我画了张图,给你解释整个归并排序的过程。

说到这里,我想问你,这个归并排序、分治和递归到底是什么关系呢?用一句话简单地说就是,归并排序使用了分治的思想,而这个过程需要使用递归来实现。
归并排序算法用分治的思想把数列不断地简化,直到每个数列仅剩下一个单独的数,然后再使用归并逐步合并有序的数列,从而达到将整个数列进行排序的目的。而这个归并排序,正好可以使用递归的方式来实现。为什么这么说?首先,我们来看看这张图,分治的过程是不是和递归的过程一致呢?

分治的过程可以通过递归来表达,因此,归并排序最直观的实现方式就是递归。所以,我们从递归的步骤出发,来看归并排序如何实现。
我们假设n=k-1的时候,我们已经对较小的两组数进行了排序。那我们只要在n=k的时候,将这两组数合并起来,并且保证合并后的数组仍然是有序的就行了。
所以,在递归的每次嵌套调用中,代码都将一组数分解成更小的两组,然后将这两个小组的排序交给下一次的嵌套调用。而本次调用只需要关心,如何将排好序的两个小组进行合并。
在初始状态,也就是n=1的时候,对于排序的案例而言,只包含单个数字的分组。由于分组里只有一个数字,所以它已经是排好序的了,之后就可以开始递归调用的返回阶段。我这里画了张图,便于你的理解。
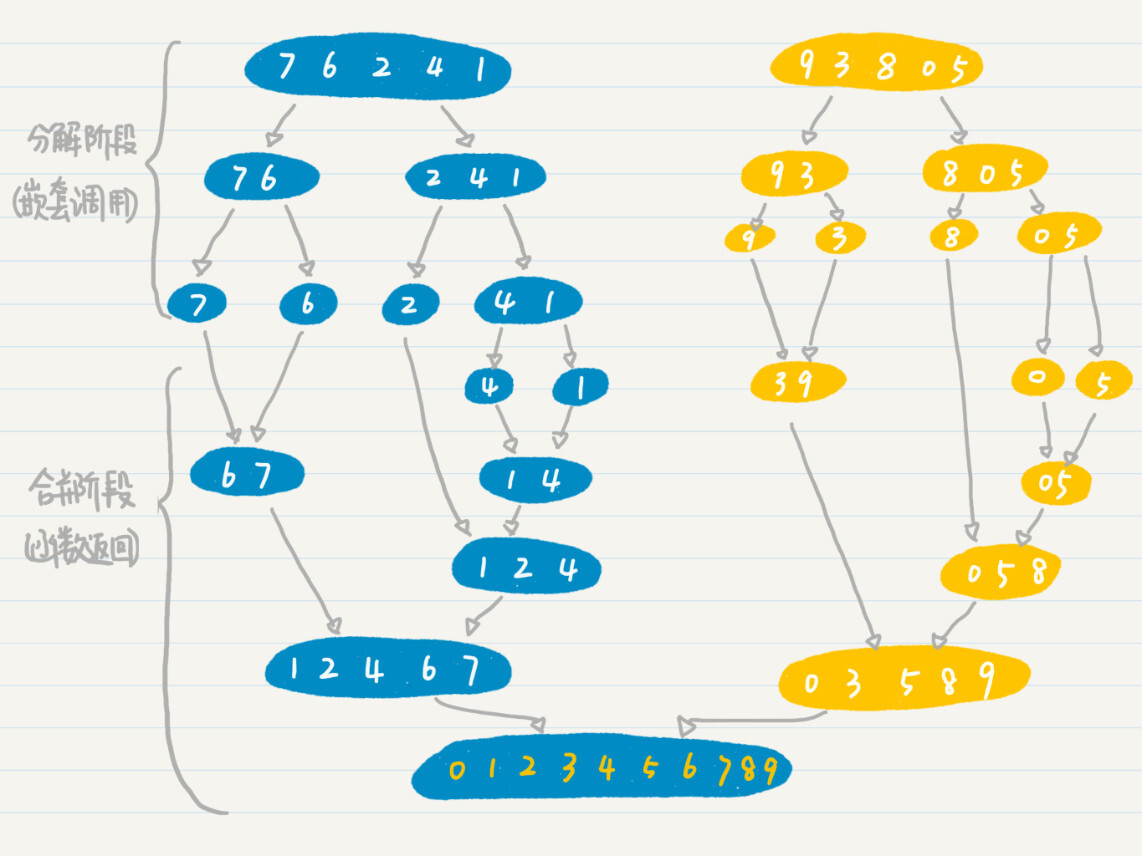
你现在应该已经明白了归并排序的基本过程,最难的已经过去了,编写代码实现就不难了。我这里给出示范性代码,你可以参考看看。
import java.util.Arrays;
public class Lesson6_1 {
/**
* @Description: 使用函数的递归(嵌套)调用,实现归并排序(从小到大)
* @param to_sort-等待排序的数组
* @return int[]-排序后的数组
*/
public static int[] merge_sort(int[] to_sort) {
if (to_sort == null) return new int[0];
// 如果分解到只剩一个数,返回该数
if (to_sort.length == 1) return to_sort;
// 将数组分解成左右两半
int mid = to_sort.length / 2;
int[] left = Arrays.copyOfRange(to_sort, 0, mid);
int[] right = Arrays.copyOfRange(to_sort, mid, to_sort.length);
// 嵌套调用,对两半分别进行排序
left = merge_sort(left);
right = merge_sort(right);
// 合并排序后的两半
int[] merged = merge(left, right);
return merged;
}
}
这里要注意一下,在归并的步骤中,由于递归的调用确保了被合并的两个较小的数组是有序的,所以我们无需比较组内的数字,只需要比较组间的数字就行了。
这个合并过程具体的实现代码是这样的:
/**
* @Description: 合并两个已经排序完毕的数组(从小到大)
* @param a-第一个数组,b-第二个数组
* @return int[]-合并后的数组
*/
public static int[] merge(int[] a, int[] b) {
if (a == null) a = new int[0];
if (b == null) b = new int[0];
int[] merged_one = new int[a.length + b.length];
int mi = 0, ai = 0, bi = 0;
// 轮流从两个数组中取出较小的值,放入合并后的数组中
while (ai < a.length && bi < b.length) {
if (a[ai] <= b[bi]) {
merged_one[mi] = a[ai];
ai ++;
} else {
merged_one[mi] = b[bi];
bi ++;
}
mi ++;
}
// 将某个数组内剩余的数字放入合并后的数组中
if (ai < a.length) {
for (int i = ai; i < a.length; i++) {
merged_one[mi] = a[i];
mi ++;
}
} else {
for (int i = bi; i < b.length; i++) {
merged_one[mi] = b[i];
mi ++;
}
}
return merged_one;
}
上述两段代码的结合,就是归并排序的递归实现。你可以用这段代码进行测试:
public static void main(String[] args) {
int[] to_sort = {3434, 3356, 67, 12334, 878667, 387};
int[] sorted = Lesson6_1.merge_sort(to_sort);
for (int i = 0; i < sorted.length; i++) {
System.out.println(sorted[i]);
}
}
分布式系统中的分治思想
聊到这里,你应该已经了解归并排序算法是如何运作的了,也对分而治之的思想有了认识。不过,分而治之更有趣的应用其实是在分布式系统中。
例如,当需要排序的数组很大(比如达到1024GB的时候),我们没法把这些数据都塞入一台普通机器的内存里。该怎么办呢?有一个办法,我们可以把这个超级大的数据集,分解为多个更小的数据集(比如16GB或者更小),然后分配到多台机器,让它们并行地处理。
等所有机器处理完后,中央服务器再进行结果的合并。由于多个小任务间不会相互干扰,可以同时处理,这样会大大增加处理的速度,减少等待时间。
在单台机器上实现归并排序的时候,我们只需要在递归函数内,实现数据分组以及合并就行了。而在多个机器之间分配数据的时候,递归函数内除了分组及合并,还要负责把数据分发到某台机器上。

在这个框架图中,你应该可以看到,分布式集群中的数据切分和合并,同单台机器上归并排序的过程是一样的,因此也是使用了分治的思想。从理论的角度来看,上面这个图很容易理解。不过在实际运用中,有个地方需要注意一下。
上图中的父结点,例如机器1、2、3,它们都没有被分配排序的工作,只是在子结点的排序完成后进行有序数组的合并,因此集群的性能没有得到充分利用。那么,另一种可能的数据切分方式是,每台机器拿出一半的数据给另一台机器处理,而自己来完成剩下一半的数据。

如果分治的时候,只进行一次问题切分,那么上述层级型的分布式架构就可以转化为类似MapReduce的架构。我画出了MapReduce的主要步骤,你可以看看,这里面有哪些步骤体现了分治的思想?

这里面主要有三个步骤用到了分治的思想。
1. 数据分割和映射
分割是指将数据源进行切分,并将分片发送到Mapper上。映射是指Mapper根据应用的需求,将内容按照键-值的匹配,存储到哈希结构中。这两个步骤将大的数据集合切分为更小的数据集,降低了每台机器节点的负载,因此和分治中的问题分解类似。不过,MapReduce采用了哈希映射来分配数据,而普通的分治或递归不一定需要。
2.归约
归约是指接受到的一组键值配对,如果是键内容相同的配对,就将它们的值归并。这和本机的递归调用后返回结果的过程类似。不过,由于哈希映射的关系,MapReduce还需要洗牌的步骤,也就是将键-值的配对不断地发给对应的Reducer进行归约。普通的分治或递归不一定需要洗牌的步骤。
3.合并
为了提升洗牌阶段的效率,可以选择减少发送到归约阶段的键-值配对。具体做法是在数据映射和洗牌之间,加入合并的过程,在每个Mapper节点上先进行一次本地的归约。然后只将合并的结果发送到洗牌和归约阶段。这和本机的递归调用后返回结果的过程类似。
说了这么多,你现在对分治应该有比较深入的理解了。实际上,分治主要就是用在将复杂问题转化为若干个规模相当的小问题上。分治思想通常包括问题的细分和结果的合并,正好对应于递归编程的函数嵌套调用和函数结果的返回。细分后的问题交给嵌套调用的函数去解决,而结果合并之后交由函数进行返回。所以,分治问题适合使用递归来实现。同时,分治的思想也可以帮助我们设计分布式系统和并行计算,细分后的问题交给不同的机器来处理,而其中的某些机器专门负责收集来自不同机器的处理结果,完成结果的合并。
小结
这两节我们学习了递归法。递归采用了和数学归纳法类似的思想,但是它用的是逆向递推,化繁为简,把复杂的问题逐步简化。再加上分治原理,我们就可以更有效地把问题细分,进行并行化的处理。
而计算机编程中的函数嵌套调用,正好对应了数学中递归的逆向递推,所以你只要弄明白了数学递推式,就能非常容易的写出对应的递归编码。这是为什么递归在编程领域有着非常广泛的应用。不过,需要注意的是,递归编程在没有开始返回结果之前,保存了大量的中间结果,所以比较消耗系统资源。这也是一般的编程语言都会限制递归的深度(也就是嵌套的次数)的原因。

思考题
你有没有想过,在归并排序的时候,为什么每次都将原有的数组分解为两组,而不是更多组呢?如果分为更多组,是否可行?
欢迎在留言区交作业,并写下你今天的学习笔记。你可以点击“请朋友读”,把今天的内容分享给你的好友,和他一起精进。

精选留言
如果不是分为两组,而是多组是可行的,但是处理起来比较麻烦。虽然分组的时候,能够更快完成,但是在合并的时候需要同时比较多组中的数据,取最小的一个。当分组数量比较大的时候,在合并的时候,为了考虑效率,需要维护一个堆来取最小值。假设分为N组,分组的时间复杂度是logn(N为底), 合并的时候时间复杂度为nlogN,总的时间复杂度不变,还是nlogn。不知道理解对不对,请老师指教!
def mergeSort(list):
if(len(list)==0):
return 0
if(len(list)==1):
return list[0]
else:
listHalfLen=int(len(list)/2)
left=mergeSort(list[0:listHalfLen])
right=mergeSort(list[listHalfLen:])
data=merge(left,right)
return data
def merge(left,right):
mid=[]
ai=0
bi=0
if(isinstance(left,int)):
leftLen=1
left=[left]
else:
leftLen=len(left)
if(isinstance(right,int)):
rightLen=1
right=[right]
else:
rightLen = len(right)
while(ai < leftLen and bi < rightLen):
if(left[ai]<right[bi]):
mid.append(left[ai])
ai+=1
else:
mid.append(right[bi])
bi+=1
if(ai< leftLen):
newleft=left[ai:]
for i in newleft:
mid.append(i)
else:
newright = right[bi:]
for i in newright:
mid.append(i)
return mid
list=[3,8,5,9,7,1,10]
mergeSort(list)
刚学python,希望大家多多指教
归并排序代码中有非空判断代码
if (a == null) a = new int[0];
if (to_sort == null) return to_sort;
什么情况下会出现数组是null??
* 采用分而治之思想实现数组排序, 递归为其实现技巧
*/
#include <iostream>
using namespace std;
void merge(int *array, int low, int mid, int high) {
// left: low ~ mid, right: mid+1 ~ high
int size = high - low + 1;
int *tmp = new int[size];
int i = low, j = mid+1, k = 0;
while (i <= mid && j <= high) {
if (array[i] <= array[j]) {
tmp[k++] = array[i++];
} else {
tmp[k++] = array[j++];
}
}
// the rest elements
while (i <= mid) {
tmp[k++] = array[i++];
}
while (j <= high) {
tmp[k++] = array[j++];
}
// copy the elements to original array
for (k = 0; k < size; ++k) {
array[k+low] = tmp[k];
}
}
void _mergeSort(int *array, int low, int high) {
if (low >= high) return;
int mid = low + ((high-low) >> 1);
_mergeSort(array, low, mid);
_mergeSort(array, mid+1, high);
merge(array, low, mid, high);
}
void mergeSort(int *array, int size) {
cout << "*****************before**************" << endl;
for (int i = 0; i < size; ++i) {
cout << array[i] << " ";
}
cout << endl;
_mergeSort(array, 0, size-1);
cout << "*****************after**************" << endl;
for (int i = 0; i < size; ++i) {
cout << array[i] << " ";
}
cout << endl;
}
int main() {
int array[] = {2, 3, 5, 1, 4, 9, 7, 6, 10};
mergeSort(array, 9);
return 0;
}
*****************before**************
2 3 5 1 4 9 7 6 10
*****************after**************
1 2 3 4 5 6 7 9 10
def split_list(temp_list):
if not isinstance(temp_list, list):
raise TypeError
else:
if not temp_list:
raise ValueError
else:
length = len(temp_list)
if length == 1:
return temp_list
import math
left = math.ceil(length / 2)
del math
left_list = split_list(temp_list[:left])
right_list = split_list(temp_list[left:])
return merger_list(left_list, right_list)
# 归并
def merger_list(left, right):
result = []
while True:
if left and right:
left_0 = left[0]
right_0 = right[0]
if left_0 > right_0:
min_num = right.pop(0)
else:
min_num = left.pop(0)
result.append(min_num)
elif left:
result.append(left.pop(0))
elif right:
result.append(right.pop(0))
else:
break
return result
print(split_list([3, 1, 2, 7, 4, 6, 9, 9, 10, 11, 4, 5]))
function guibingorder(arr) {
if (arr.length > 1) {
var leftarr = [];
var rightarr = [];
var splitindex = Math.floor(arr.length / 2);
leftarr = arr.slice(0, splitindex);
rightarr = arr.slice(splitindex, arr.length);
leftarr = arguments.callee(leftarr);
rightarr = arguments.callee(rightarr);
var result = [];
while (Math.max(leftarr.length, rightarr.length) > 0) {
//右边遍历完了 或者 左边比右边的小,则 从左边取出来
if (rightarr.length == 0 || leftarr[0] < rightarr[0]) {
result.push(leftarr[0]);
leftarr.splice(0, 1);
} else {
result.push(rightarr[0]);
rightarr.splice(0, 1);
}
}
return result;
}
return arr;
}
# 切分
def split_list(temp_list):
if not isinstance(temp_list, list):
raise TypeError
else:
if not temp_list:
raise ValueError
else:
length = len(temp_list)
if length == 1:
return temp_list
import math
left = math.ceil(length / 2)
del math
left_list = split_list(temp_list[:left])
right_list = split_list(temp_list[left:])
return merger_list(left_list, right_list)
# 归并
def merger_list(left, right):
result = []
while True:
if left and right:
left_0 = left[0]
right_0 = right[0]
if left_0 > right_0:
min_num = right.pop(0)
else:
min_num = left.pop(0)
result.append(min_num)
elif left:
result.append(left.pop(0))
elif right:
result.append(right.pop(0))
else:
break
return result
print(split_list([3, 1, 2, 7, 4, 6, 9, 9, 10, 11, 4, 5]))
#include <iostream>
#include <vector>
using namespace std;
// 拷贝数组函数
// 将数组SourceData的第BeginIndex个元素~第EndIndex个元素拷贝到另一个数组中,并返回
template <class T>
vector<T> CopyVectorData(vector<T> &SourceData, int BeginIndex, int EndIndex)
{
vector<T> tempVec;
for (int i = BeginIndex; i <= EndIndex; ++i)
{
tempVec.push_back(SourceData[i]);
}
return tempVec;
}
// 合并函数
// 将两个数组中的元素按照从小到大的形式放到另一个数组中,并返回
template <class T>
vector<T> Merge(vector<T> &LeftData, vector<T> &RightData)
{
size_t leftIndex = 0;
size_t rightIndex = 0;
vector<T> resultData;
while( (leftIndex < LeftData.size()) && (rightIndex < RightData.size()))
{
if ( LeftData[leftIndex] <= RightData[rightIndex])
{
resultData.push_back(LeftData[leftIndex]);
++leftIndex;
}
else
{
resultData.push_back(RightData[rightIndex]);
++rightIndex;
}
}
while(leftIndex < LeftData.size())
{
resultData.push_back(LeftData[leftIndex]);
++leftIndex;
}
while(rightIndex < RightData.size())
{
resultData.push_back(RightData[rightIndex]);
++rightIndex;
}
return resultData;
}
// 归并排序 算法
template <class T>
vector<T> MergeSort(vector<T> &SortData)
{
if (SortData.size() == 1)
{
return SortData;
}
vector<T> leftData = CopyVectorData(SortData, 0, SortData.size()/2 - 1);
vector<T> rightData = CopyVectorData(SortData, SortData.size()/2, SortData.size()-1);
vector<T> resultData = Merge(MergeSort(leftData), MergeSort(rightData));
return resultData;
}
int _tmain(int argc, _TCHAR* argv[])
{
int ia[] = {12, 20, 5, 10, 34, 49, 33, 88, 42, 12};
vector<int> Select(ia, ia+10);
vector<int> Result = MergeSort(Select);
system("pause");
return 0;
}
“归并排序通过分治的思想,把长度为 n 的数列,每次简化为两个...只需要 log2n 次归并。”
这句话,需要的归并次数是我算着是: 简化的组数:1,2^1,2^2..2^k。归并的时候,应该合并2^0+2^1+2^2+..+2^(k-1)次,也就是2^k-1次。我这么想对吗,老师。