
你好,我是黄申。
上一篇讲组合的时候,我最后提到了有关文本的关键字查询。今天我接着文本搜索的话题,来聊聊查询推荐(Query Suggestion)的实现过程,以及它所使用的数学思想,动态规划(Dynamic Programming)。
那什么是动态规划呢?在递归那一节,我说过,我们可以通过不断分解问题,将复杂的任务简化为最基本的小问题,比如基于递归实现的归并排序、排列和组合等。不过有时候,我们并不用处理所有可能的情况,只要找到满足条件的最优解就行了。在这种情况下,我们需要在各种可能的局部解中,找出那些可能达到最优的局部解,而放弃其他的局部解。这个寻找最优解的过程其实就是动态规划。
动态规划需要通过子问题的最优解,推导出最终问题的最优解,因此这种方法特别注重子问题之间的转移关系。我们通常把这些子问题之间的转移称为状态转移,并把用于刻画这些状态转移的表达式称为状态转移方程。很显然,找到合适的状态转移方程,是动态规划的关键。
因此,这两节我会通过实际的案例,给你详细解释如何使用动态规划法寻找最优解,包括如何分解问题、发现状态转移的规律,以及定义状态转移方程。
编辑距离
当你在搜索引擎的搜索框中输入单词的时候,有没有发现,搜索引擎会返回一系列相关的关键词,方便你直接点击。甚至,当你某个单词输入有误的时候,搜索引擎依旧会返回正确的搜索结果。
搜索下拉提示和关键词纠错,这两个功能其实就是查询推荐。查询推荐的核心思想其实就是,对于用户的输入,查找相似的关键词并进行返回。而测量拉丁文的文本相似度,最常用的指标是编辑距离(Edit Distance)。
我刚才说了,查询推荐的这两个功能是针对输入有缺失或者有错误的字符串,依旧返回相应的结果。那么,将错误的字符串转成正确的,以此来返回查询结果,这个过程究竟是怎么进行的呢?
由一个字符串转成另一个字符串所需的最少编辑操作次数,我们就叫作编辑距离。这个概念是俄罗斯科学家莱文斯坦提出来的,所以我们也把编辑距离称作莱文斯坦距离(Levenshtein distance)。很显然,编辑距离越小,说明这两个字符串越相似,可以互相作为查询推荐。编辑操作有这三种:把一个字符替换成另一个字符;插入一个字符;删除一个字符。
比如,我们想把mouuse转换成mouse,有很多方法可以实现,但是很显然,直接删除一个“u”是最简单的,所以这两者的编辑距离就是1。
状态转移
对于mouse和mouuse的例子,我们肉眼很快就能观察出来,编辑距离是1。但是我们现实的场景中,常常不会这么简单。如果给定任意两个非常复杂的字符串,如何高效地计算出它们之间的编辑距离呢?
我们之前讲过排列和组合。我们先试试用排列的思想来进行编辑操作。比如,把一个字符替换成另一个字符,我们可以想成把A中的一个字符替换成B中的一个字符。假设B中有m个不同的字符,那么替换的时候就有m种可能性。对于插入一个字符,我们可以想成在A中插入来自B的一个字符,同样假设B中有m个不同的字符,那么也有m种可能性。至于删除一个字符,我们可以想成在A中删除任何一个字符,假设A有n个不同的字符,那么有n种可能性。
可是,等到实现的时候,你会发现实际情况比想象中复杂得多。
首先,计算量非常大。我们假设字符串A的长度是n,而B字符串中不同的字符数量是m,那么A所有可能的排列大致在m^n这个数量级,这会导致非常久的处理时间。对于查询推荐等实时性的服务而言,服务器的响应时间太长,用户肯定无法接受。
其次,如果需要在字符串A中加字符,那么加几个呢,加在哪里呢?同样,删除字符也是如此。因此,可能的排列其实远不止m^n。
我们现在回到问题本身,其实编辑距离只需要求最小的操作次数,并不要求列出所有的可能。而且排列过程非常容易出错,还会浪费大量计算资源。看来,排列的方法并不可行。
好,这里再来思考一下,其实我们并不需要排列的所有可能性,而只是关心最优解,也就是最短距离。那么,我们能不能每次都选择出一个到目前为止的最优解,并且只保留这种最优解?如果是这样,我们虽然还是使用迭代或者递归编程来实现,但效率上就可以提升很多。
我们先考虑最简单的情况。假设字符串A和B都是空字符串,那么很明显这个时候编辑距离就是0。如果A增加一个字符a1,B保持不动,编辑距离就增加1。同样,如果B增加一个字符b1,A保持不动,编辑距离增加1。但是,如果A和B有一个字符,那么问题就有点复杂了,我们可以细分为以下几种情况。
我们先来看插入字符的情况。A字符串是a1的时候,B空串增加一个字符变为b1;或者B字符串为b1的时候,A空串增加一个字符变为a1。很明显,这种情况下,编辑距离都要增加1。
我们再来看替换字符的情况。当A和B都是空串的时候,同时增加一个字符。如果要加入的字符a1和b1不相等,表示A和B之间转化的时候需要替换字符,那么编辑距离就是加1;如果a1和b1相等,无需替换,那么编辑距离不变。
最后,我们取上述三种情况中编辑距离的最小值作为当前的编辑距离。注意,这里我们只需要保留这个最小的值,而舍弃其他更大的值。这是为什么呢?因为编辑距离随着字符串的增长,是单调递增的。所以,要求最终的最小值,必须要保证对于每个子串,都取得了最小值。有了这点,之后我们就可以使用迭代的方式,一步步推导下去,直到两个字符串结束比较。
刚才我说的情况中没有删除,这是因为删除就是插入的逆操作。如果我们从完整的字符串A或者B开始,而不是从空串开始,这就是删除操作了。
从上述的过程可以看出,我们确实可以把求编辑距离这个复杂的问题,划分为更多更小的子问题。而且,更为重要的一点是,我们在每一个子问题中,都只需要保留一个最优解。之后的问题求解,只依赖这个最优值。这种求编辑距离的方法就是动态规划,而这些子问题在动态规划中被称为不同的状态。
如果文字描述不是很清楚的话,我这里又画一张表,把各个状态之间的转移都标示清楚,你就一目了然了。
我还是用mouuse和mouse的例子。我把mouuse的字符数组作为表格的行,每一行表示其中一个字母,而mouse的字符数组作为列,每列表示其中一个字母,这样就得到下面这个表格。

这张表格里的不同状态之间的转移,就是状态转移。其中红色部分表示字符串演变(或者说状态转移)的方式以及相应的编辑距离计算。对于表格中其他空白的部分,我暂时不给出,你可以试着自己来推导。
编辑距离是具有对称性的,也就是说从字符串A到B的编辑距离,和从字符串B到A的编辑距离,两者一定是相等的。这个应该很好理解。
你可以把刚才那个状态转移表的行和列互换一下,再推导一下,看看得出的编辑距离是否还是1。我现在从理论上解释下这一点。这其实是由编辑距离的三种操作决定的。比如说,从字符串A演变到B的每一种操作,都可以转换为从字符串B演变到A的某一种操作。
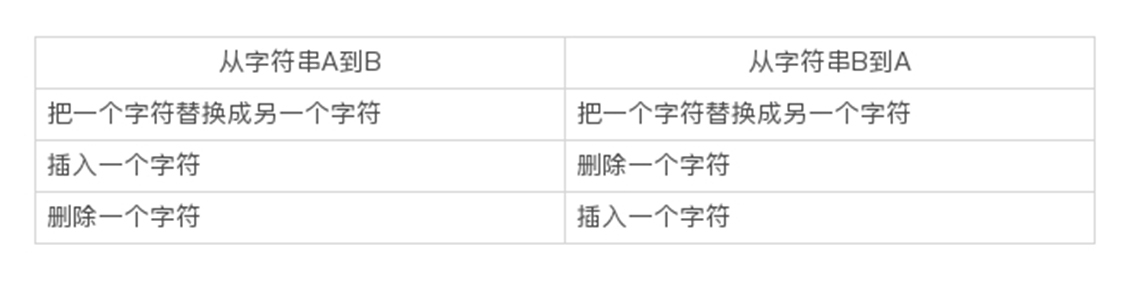
所以说,从字符串A演变到B的每一种变化方式,都可以找到对应的从字符串B演变到A的某种方式,两者的操作次数一样。自然,代表最小操作次数的编辑距离也就一样了。
小结
我今天介绍了用于查询推荐的编辑距离。编辑距离的定义很好理解,不过,求任意两个字符串之间的编辑距离可不是一件容易的事情。我先尝试用排列来分析问题,发现这条路走不通,而后我们仍然使用了化繁为简的思路,把编辑距离的计算拆分为3种情况,并建立了子串之间的联系。
你不要觉得这样的分析过程比较繁琐,我想说的是,学数学固然是为了得到结果,但是学习的过程,是要学会解决问题的方法和思路。比如面对一个问题的时候,你可能不知道用什么方法来解决,但是你可以尝试用我们学过的这些基础思想去分析,去比对,在这个分析的过程中去总结这些方法的使用规律,久而久之,你就能摸索出自己解决问题的套路。
比如说,动态规划虽然也采用了把问题逐步简化的思想,但是它和基于递归的归并排序、排列组合等解法有所不同。能够使用动态规划解决的问题,通常只关心一个最优解,而这个最优解是单调改变的,例如最大值、最小值等等。因此,动态规划中的每种状态,通常只保留一个当前的最优解,这也是动态规划效率比较高的原因。

思考题
理解了动态规划法和状态转移之后,你觉得根据编辑距离来衡量字符串之间的相似程度有什么局限性?你有什么优化方案吗?
欢迎在留言区交作业,并写下你今天的学习笔记。你可以点击“请朋友读”,把今天的内容分享给你的好友,和他一起精进。

精选留言
1、A、B都为空A转化为B或者B转化为A不需要做任何操作编辑距离为0(可以理解)
2、A增加一个字符a1,B保持不动,编辑距离为1。或者B增加一个字符b1,A保持不动,编辑距离为1.(初始为空的情况,可以理解)
3、如何A和B有一个字符那么情况就有点复杂了,具体如下:
(1)插入字符的情况,A字符串为a1的时候,B空串增加一个字符变为b1,或者B字符串为b1的时候,A空串增加一个字符变为a1。很明显这种情况下编辑距离都要增加1
问题:这时候如果b1和a1是一样的字符A或者B再插入后已经是一样的了也不需要再做转化了,这时候编辑距离是否应该就是1?下面的表格中A、B串的m与m处的插入情况与这里一样插入的编辑距离为什么是2?
(2)替换字符的情况,可以理解为不相等的情况下才替换所以此时编辑距离加1,如果相等不需要替换则编辑距离为0?
麻烦老师解答一下,谢谢!
比如mouse就是用户输入mouuse的相似字符串。
一个字符串有哪些相似字符串,无非是把该字符串进行一系列可能的变形编辑。比如把某个字母删掉,或增加一个字母,或替换该字母
最后看变形后的单词,是否是一个合法单词。如果是,则给用户提示。
原始单词或字符变形到一个合法字符串的步数,称为这两个单词之间的编辑距离。
但一个单词随着长度增加,其对应的合法单词,编辑距离计算将会很多。不可取。
所以需要最优解,找出用户输入词,编辑距离最小的目标词即可
2.分析到总体编辑距离是2,2,0,后边总结又说1,1,0
麻烦老师能不能把步骤分解解释一下
工作和生活中,我们一般把大问题分解为小问题,再把小问题 分解为容易解答的问题,动态规划 就是在 容易解答的问题中选择最优解。
黄老师 在文中提到:搜索引擎输入的搜索词的查询和推荐,就是对 缺失和错误的字符串进行操作,比如我们输入错误的字符串A,和正确的字符串B,需要把字符串A改到B,需要把字符串 分解到字符 的小问题,然后进行‘增、删、改’等操作,这里运用 动态规划 寻找最优解,不需要使用排列 这么复杂的方法 因为排列计算消耗的时间会很长,运用动态规划 很节能。
今天所得:解决问题的方法 (1)不断的分解问题,把大问题分解为小问题,把小问题 再分解...直至到可以解答的问题;(2)使用动态规划 求解 小问题的 最优解。
回答老师的问题:用编辑距离对字符串状态转移资源消耗的标记,会浪费很多 内存和运算资源,可以把 字符串 再分割成字符,把 二个字符串的不同的字符 掏出来,再用编辑距离 处理,应该会更快一下、占用资源也少一些,老师是否同意,也期待 黄老师的指正。
老师 可以用 斐波那契数列 来说明 动态规划的问题,更让我们易理解。
如果推导表格往下移动一格,字符串A变成mo,字符串B变成了m,这时应该如何推导啊?希望您帮忙解答一下,第一次实际接触动态规划,谢谢!
最近反复看这两篇动态规划,表格推导看的有点似懂非懂。望老师指导一下
但是老师,也有另外一个思路感觉和上面我说的有点相悖。比如字符 mouuse 最终要匹配上 mouse,正确的单词mouse已经是存在的,我们只是拿用户输入的字符去匹配现成的合法单词,所以用户输入的m(字符A),字符B是已经存在的了,因此不存在字符A和字符B同时为空的情况,那么就只需要字符A插入m即可,如果是这样的话,m行m列理解起来最大编辑距离也确实是1才对!
本节:三种编辑距离 2,2,0。最后一个是替换。
替换操作理解,插入和删除不理解。老师帮忙分析下。
一种情况:
A字符为:m B字符为:mo
第二种情况:
A字符为:mo B字符为:mo
其它衡量字符串的相似性指标有:余弦相似性和欧式距离,之前做自然语言处理有所了解,但也不怎么清楚,麻烦老师解答下。谢谢
using namespace std;
void levenshteinDis(const char* str1, const char* str2, int m, int n,
int i, int j, int edist, int &mind) {
if (i == m || j == n) {
if (i < m) edist += (m-i);
if (j < n) edist += (n-j);
if (edist < mind) mind = edist;
return;
}
if (str1[i] == str2[j]) {
levenshteinDis(str1, str2, m, n, i+1, j+1, edist, mind);
} else {
// 删除或增加
levenshteinDis(str1, str2, m, n, i+1, j, edist+1, mind);
levenshteinDis(str1, str2, m, n, i, j+1, edist+1, mind);
// 替换操作
levenshteinDis(str1, str2, m, n, i+1, j+1, edist+1, mind);
}
}
int levenshteinDis(const char* a, const char* b, int m, int n) {
int mind = 0xfffffff;
levenshteinDis(a, b, m, n, 0, 0, 0, mind);
return mind;
}
/*
* 状态转移方程
* 1.当a[i] != b[j], min_edist(i,j) = min(min_edist(i-1,j)+1, min_edist(i,j-1)+1, min_edist(i-1, j-1)+1)
* 2.当a[i] == b[j], min_edist(i,j) = min(min_edist(i-1,j)+1, min_edist(i,j-1)+1, min_edist(i-1, j-1))
*/
int levenshteinDisDP(const char* a, const char* b, int m, int n) {
// 初始化dp数组
int dp[m][n];
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
dp[i][j] = 0;
}
}
// 初始化第0列
for (int i = 0; i < m; ++i) {
if (a[i] == b[0]) dp[i][0] = i;
else if (i != 0) dp[i][0] = dp[i-1][0] + 1;
else dp[i][0] = 1;
}
// 初始化第0行
for (int i = 0; i < n; ++i) {
if (a[0] == b[i]) dp[0][i] = i;
else if (i > 0) dp[0][i] = dp[0][i-1] + 1;
else dp[0][i] = 1;
}
// 填表余下部分
for (int i = 1; i < m; ++i) {
for (int j = 1; j < n; ++j) {
dp[i][j] = min(dp[i-1][j]+1, dp[i][j-1]+1,
a[i] == b[j] ? dp[i-1][j-1]:dp[i-1][j-1]+1);
}
}
return dp[m-1][n-1];
}