
你好,我是黄申。
上一节,我们探讨了如何在树的结构里进行深度优先搜索。说到这里,有一个问题,不知道你有没有思考过,树既然是两维的,我们为什么一定要朝着纵向去进行深度优先搜索呢?是不是也可以朝着横向来进行搜索呢?今天我们就来看另一种搜索机制,广度优先搜索。
社交网络中的好友问题
LinkedIn、Facebook、微信、QQ这些社交网络平台都有大量的用户。在这些社交网络中,非常重要的一部分就是人与人之间的“好友”关系。
在数学里,为了表示这种好友关系,我们通常使用图中的结点来表示一个人,而用图中的边来表示人和人之间的相识关系,那么社交网络就可以用图论来表示。而“相识关系”又可以分为单向和双向。
单向表示,两个人a和b,a认识b,但是b不认识a。如果是单向关系,我们就需要使用有向边来区分是a认识b,还是b认识a。如果是双向关系,双方相互认识,因此直接用无向边就够了。在今天的内容里,我们假设相识关系都是双向的,所以我们今天讨论的都是无向图。
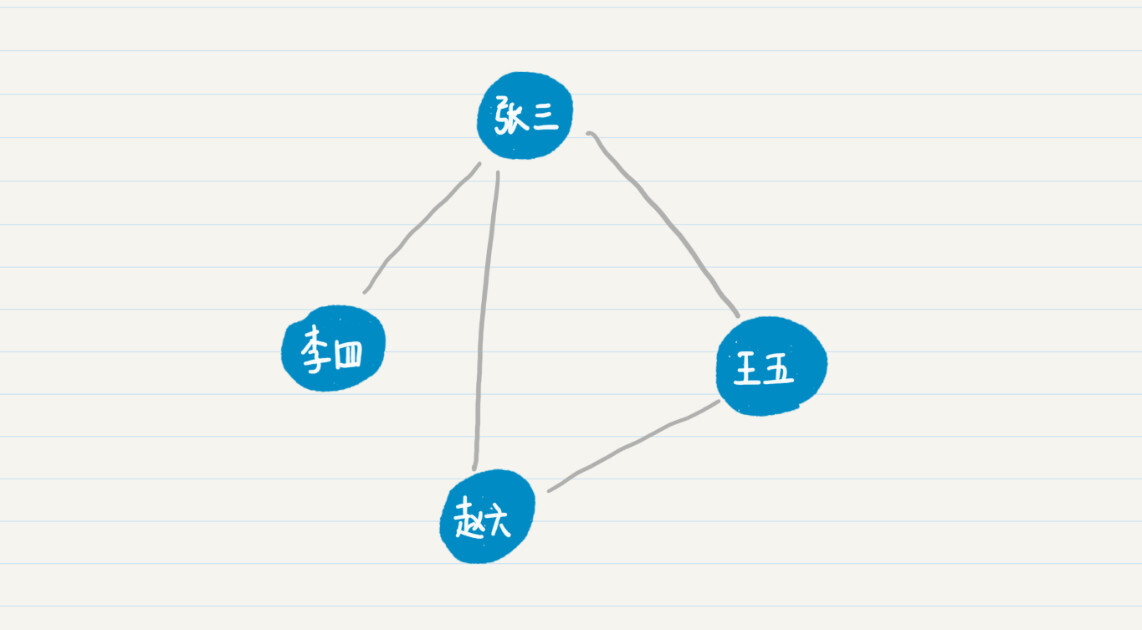
从上面的例图可以看出,人与人之间的相识关系,可以有多条路径。比如,张三可以直接连接赵六,也可以通过王五来连接赵六。比较这两条通路,最短的通路长度是1,因此张三和赵六是一度好友。也就是说,这里我用两人之间最短通路的长度,来定义他们是几度好友。照此定义,在之前的社交关系示意图中,张三、王五和赵六互为一度好友,而李四和赵六、王五为二度好友。
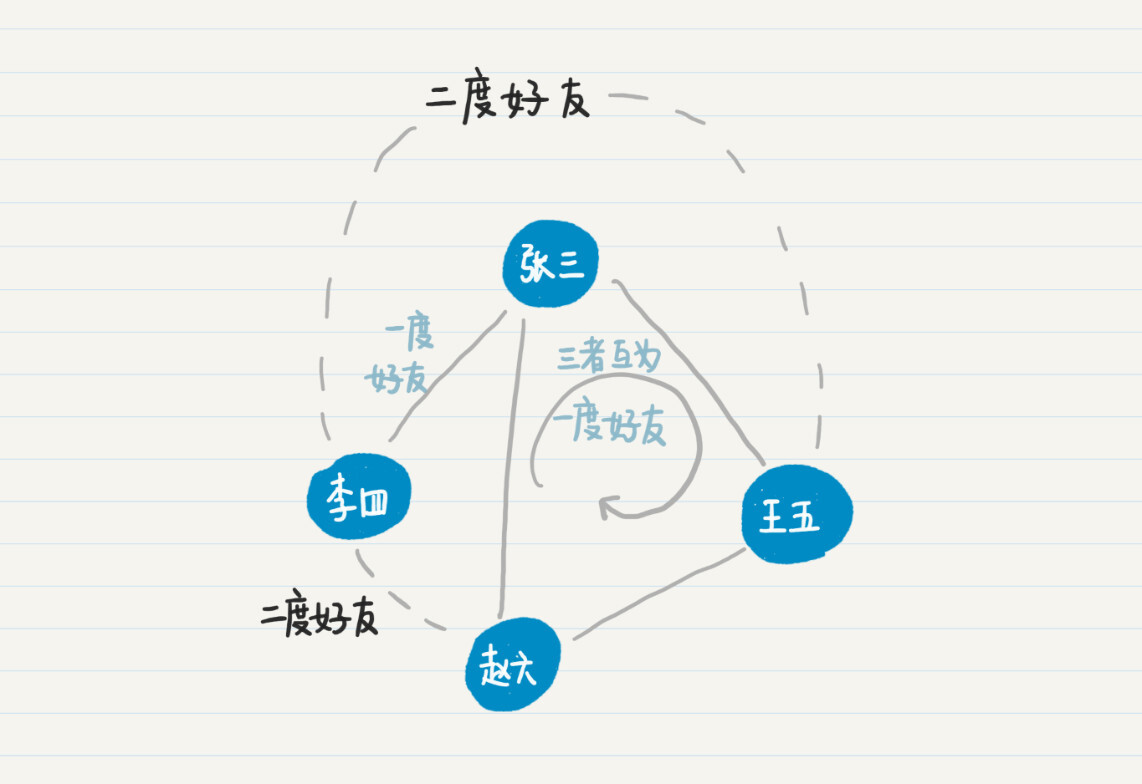
寻找两个人之间的最短通路,或者说找出两人是几度好友,在社交中有不少应用。例如,向你推荐新的好友、找出两人之间的关系的紧密程度、职场背景调查等等。在LinkedIn上,有个功能就是向你推荐了你可能感兴趣的人。下面这张图是我的LinkedIn主页里所显示的好友推荐。
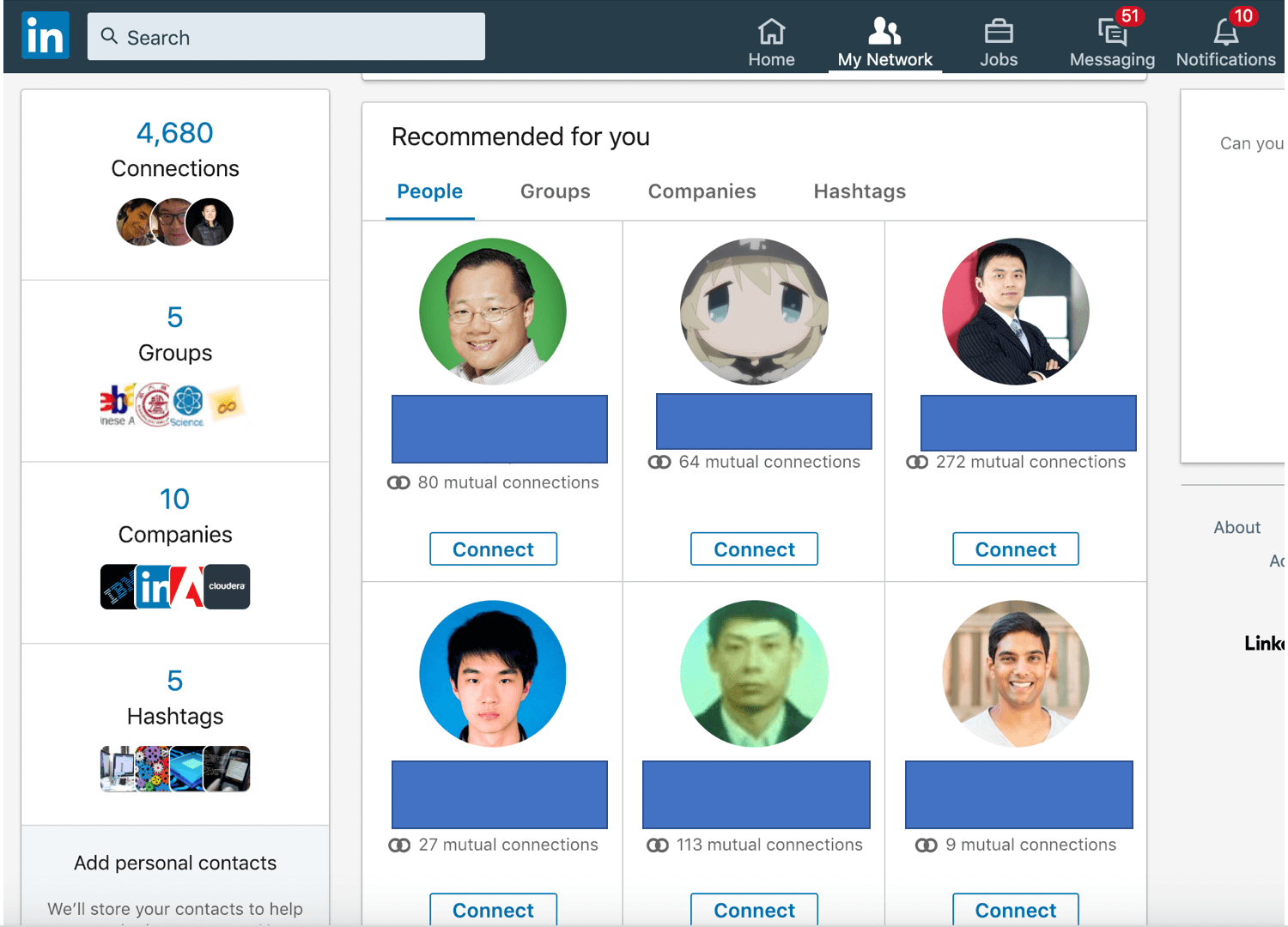
这些被推荐的候选人,和我都有不少的共同连接,也就是共同好友。所以他们都是我的二度好友。但是,他们和我之间还没有建立直接的联系,因此不是一度好友。也就是说,对于某个当前用户,LinkedIn是这么来选择好友推荐的:
-
被推荐的人和当前用户不是一度好友;
-
被推荐的人和当前用户是二度好友。
那为什么我们不考虑“三度“甚至是“四度”好友呢?我前面已经说过,两人之间最短的通路长度,表示他们是几度好友。那么三度或者四度,就意味着两人间最短的通路也要经历2个或更多的中间人,他们的关系就比较疏远,互相添加好友的可能性就大大降低。
所以呢,总结一下,如果我们想进行好友推荐,那么就要优先考虑用户的“二度“好友,然后才是“三度”或者“四度”好友。那么,下一个紧接着要面临的问题就是:给定一个用户,如何优先找到他的二度好友呢?
深度优先搜索面临的问题
这种情况下,你可能会想到上一篇介绍的深度优先搜索。深度优先搜索不仅可以用在树里,还可以应用在图里。不过,我们要面临的问题是图中可能存在回路,这会增加通路的长度,这是我们在计算几度好友时所不希望的。所以在使用深度优选搜索的时候,一旦遇到产生回路的边,我们需要将它过滤。具体的操作是,判断新访问的点是不是已经在当前通路中出现过,如果出现过就不再访问。
如果过滤掉产生回路的边,从一个用户出发,我们确实可以使用深度优先的策略,搜索完他所有的n度好友,然后再根据关系的度数,从二度、三度再到四度进行排序。这是个解决方法,但是效率太低了。为什么呢?
你也许听说过社交关系的六度理论。这个理论神奇的地方在于,它说地球上任何两个人之间的社交关系不会超过六度。咋一听,感觉不太可能。仔细想想,假设每个人平均认识100个人(我真心不觉得100很多,不信你掰着指头数数看自己认识多少人),那么你的二度好友就是100^2,这个可以用我们前面讲的排列思想计算而来。
以此类推,三度好友是100^3,到五度好友就有100亿人了,已经超过了地球目前的总人口。即使存在一些好友重复的情况下,例如,你的一度好友可能也出现在你的三度好友中,那这也不可能改变结果的数量级。所以目前来看,地球上任何两个人之间的社会关系不会超过六度。
六度理论告诉我们,你的社会关系会随着关系的度数增加,而呈指数级的膨胀。这意味着,在深度搜索的时候,每增加一度关系,就会新增大量的好友。但是你仔细回想一下,当我们在用户推荐中查看可能的好友时,基本上不会看完所有推荐列表,最多也就看个几十个人,一般可能也就看看前几个人。所以,如果我们使用深度优先搜索,把所有可能的好友都找到再排序,那效率实在太低了。
什么是广度优先搜索?
更高效的做法是,我们只需要先找到所有二度的好友,如果二度好友不够了,再去找三度或者四度的好友。这种好友搜索的模式,其实就是我们今天要介绍的广度优先搜索。
广度优先搜索(Breadth First Search),也叫宽度优先搜索,是指从图中的某个结点出发,沿着和这个点相连的边向前走,去寻找和这个点距离为1的所有其他点。只有当和起始点距离为1的所有点都被搜索完毕,才开始搜索和起始点距离为2的点。当所有和起始点距离为2的点都被搜索完了,才开始搜索和起始点距离为3的点,如此类推。
我用上一节介绍深度优先搜索顺序的那棵树,带你看一下广度优先搜索和深度优先搜索,在结点访问的顺序上有什么不一样。
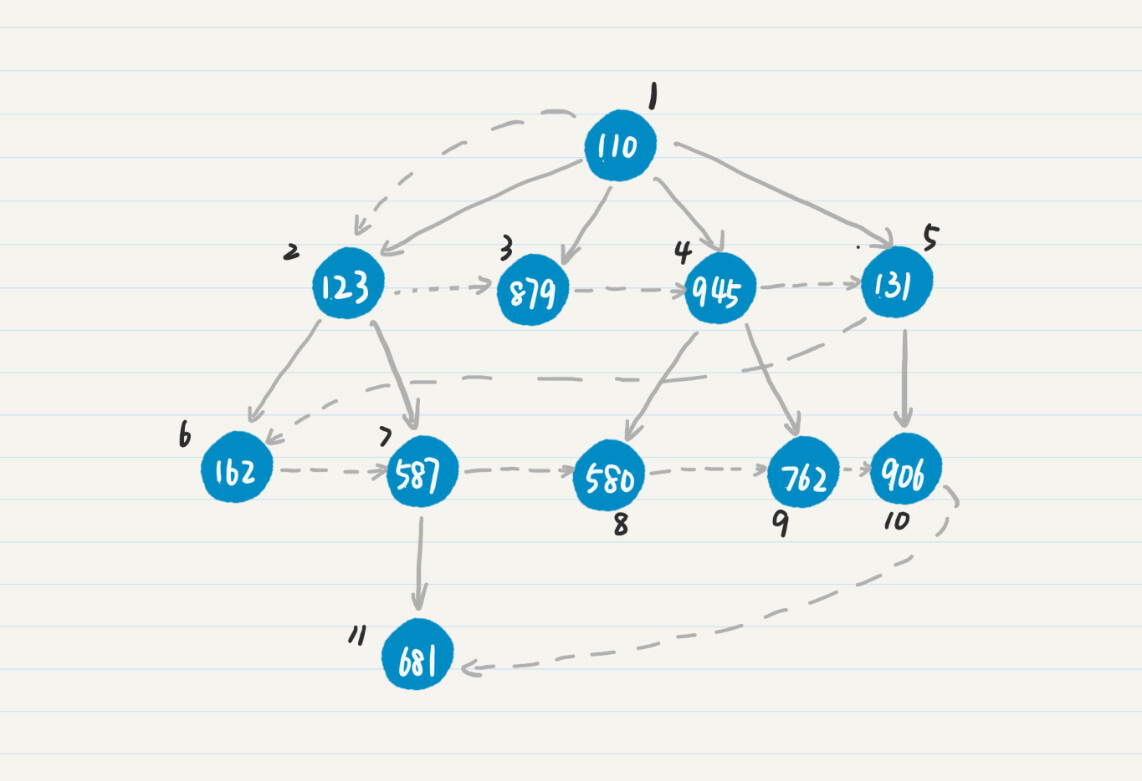
同样,我们用结点上的数字表示结点的ID,用虚线表示遍历前进的方向,用结点边上的数字表示该结点在广度优先搜索中被访问的顺序。从这个图中,你有没有发现,广度优先搜索其实就是横向搜索一颗树啊!
尽管广度优先和深度优先搜索的顺序是不一样的,它们也有两个共同点。
第一,在前进的过程中,我们不希望走重复的结点和边,所以会对已经被访问过的点做记号,而在之后的前进过程中,就只访问那些还没有被标记的点。这一点上,广度优先和深度优先是一致的。有所不同的是,在广度优先中,如果发现和某个结点直接相连的点都已经被访问过,那么下一步就会看和这个点的兄弟结点直接相连的那些点,从中看看是不是有新的点可以访问。
例如,在上图中,访问完结点945的两个子结点580和762之后,广度优先策略发现945没有其他的子结点了,因此就去查看945的兄弟结点131,看看它有哪些子结点可以访问,因此下一个被访问的点是906。而在深度优先中,如果到了某个点,发现和这个点直接相连的所有点都已经被访问过了,那么不会查看它的兄弟结点,而是回退到这个点的父节点,继续查看和父结点直接相连的点中是不是存在新的点。例如在上图中,访问完结点945的两个子结点之后,深度优先策略会回退到点110,然后访问110的子结点131。
第二,广度优先搜索也可以让我们访问所有和起始点相通的点,因此也被称为广度优先遍历。如果一个图包含多个互不连通的子图,那么从起始点开始的广度优先搜索只能涵盖其中一个子图。这时,我们就需要换一个还没有被访问过的起始点,继续深度优先遍历另一个子图。深度优先搜索可以使用同样的方式来遍历有多个连通子图的图,这也回答了上一讲的思考题。
如何实现社交好友推荐?
第12讲中我说深度优先是利用递归的嵌套调用、或者是栈的数据结构来实现的。然而,广度优先的访问顺序是不一样的,我们需要优先考虑和某个给定结点距离为1的所有其他结点。等距离为1的结点访问完,才会考虑距离为2的结点。等距离为2的结点访问完,才会考虑距离为3的结点等等。在这种情况下,我们无法不断地根据结点的边走下去,而是要先遍历所有距离为1的点。
那么,如何在记录所有已被发现的结点情况下,优先访问距离更短的点呢?仔细观察,你会发现和起始点更近的结点,会先更早地被发现。也就是说,越早被访问到的结点,越早地处理它,这是不是很像我们平时排队的情形?早到的人可以优先接受服务,而晚到的人需要等前面的人都离开,才能轮到。所以这里我们需要用到队列这种先进先出(First In First Out)的数据结构。
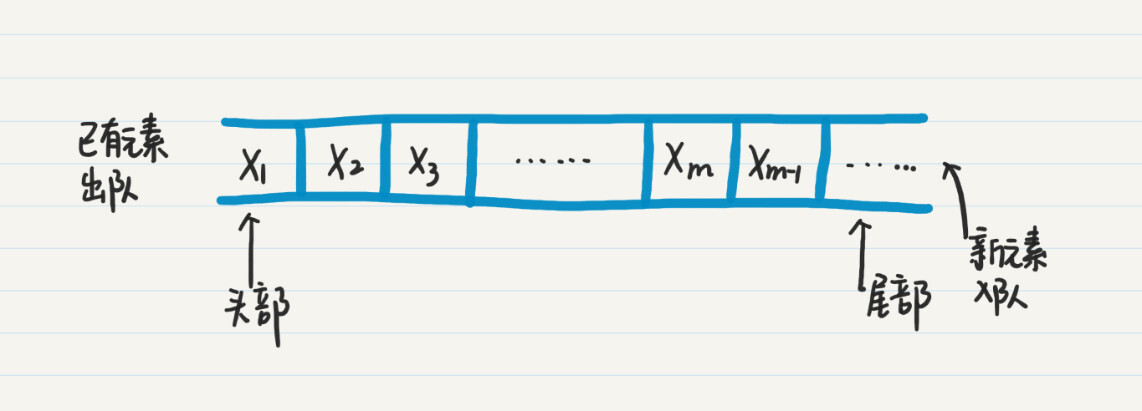
如果你不是很熟悉队列的数据结构,我这里简短地回顾一下。队列是一种线性表,要被访问的下一个元素来自队列的头部,而所有新来的元素都会加入队列的尾部。
我画了张图给你讲队列的工作过程。首先,读取已有元素的时候,都是从队列的头部来取,例如$x_{1}$,$x_{2}$等等。所有新的元素都加入队列的尾部,例如$x_{m}$,$x_{m+1}$。
那么在广度优先搜索中,队列是如何工作的呢?这主要分为以下几个步骤。
首先,把初始结点放入队列中。然后,每次从队列首位取出一个结点,搜索所有在它下一级的结点。接下来,把新发现的结点加入队列的末尾。重复上述的步骤,直到没有发现新的结点为止。
我以上面的树状图为例,并通过队列实现广度优先搜索。
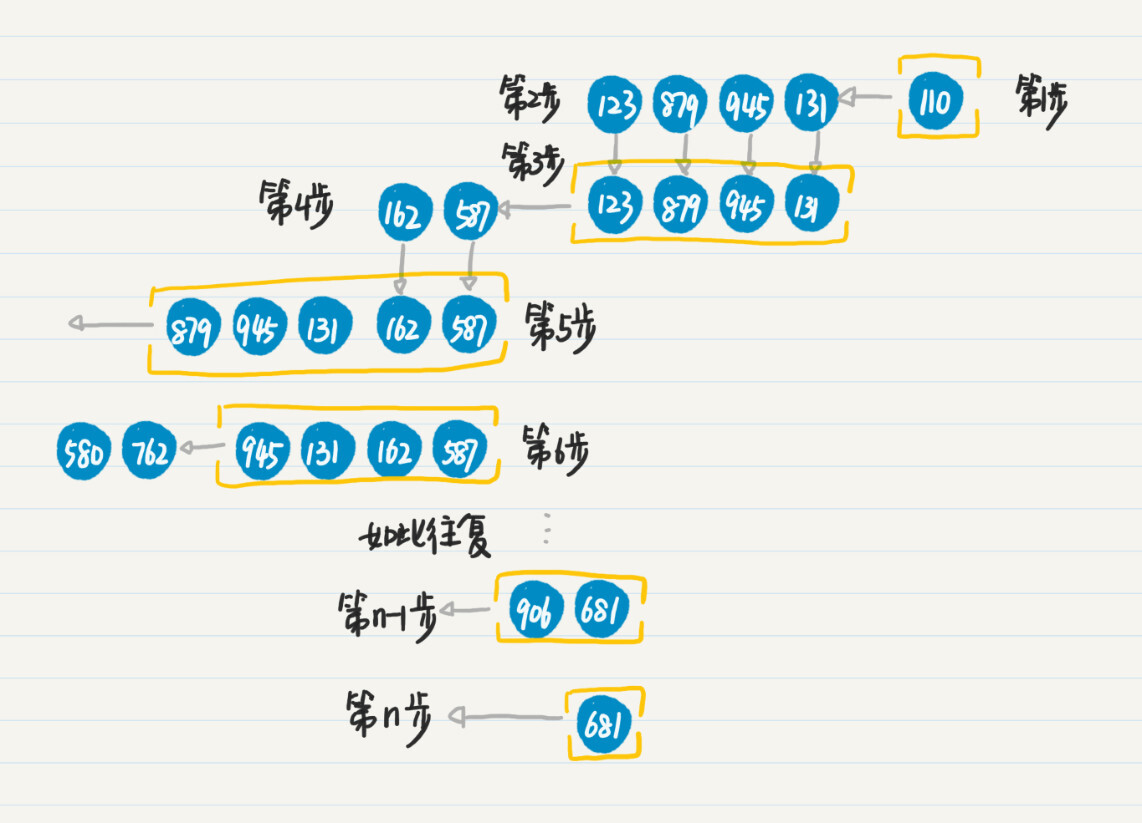
第1步,将初始结点110加入队列中。
第2步,取出结点110,搜出下一级结点123、879、945和131。
第3步,将点123、879、945和131加入队列的末尾。
第4步,重复第2和第3步,处理结点123,将新发现结点162和587加入队列末尾。
第5步,重复第2和第3步,处理结点879,没有发现新结点。
第6步,重复第2和第3步,处理结点945,将新发现的结点580和762加入队列末尾。
……
第n-1步,重复第2和第3步,处理结点906,没有发现新结点。
第n步,重复第2和第3步,处理结点681,没有发现新的结点,也没有更多待处理的结点,整个过程结束。
理解了如何使用队列来实现广度优先搜索之后,我们就可以开始着手编写代码。我们现在没有现成的用户关系网络数据,所以我们需要先模拟生成一些用户结点及其间的相识关系,然后利用队列的数据结构进行广度优先的搜索。基于此,主要使用的数据结构包括:
-
用户结点Node。这次设计的用户结点和前缀树结点TreeNode略有不同,包含了用户的ID user_id,以及这个用户的好友集合。我用HashSet实现,便于在生成用户关系图的时候,确认是否会有重复的好友。
-
表示整个图的结点数组Node[]。由于每个用户使用user_id来表示,所以我可以使用连续的数组表示所有的用户。用户的user_id就是数组的下标。
-
队列Queue。由于Java中Queue是一个接口,因此需要用一个拥有具体实现的LinkedList类。
首先我们列出结点Node类的示例代码。
public class Node {
public int user_id; // 结点的名称,这里使用用户id
public HashSet<Integer> friends = null;
// 使用哈希映射存放相连的朋友结点。哈希便于确认和某个用户是否相连。
public int degree; // 用于存放和给定的用户结点,是几度好友
// 初始化结点
public Node(int id) {
user_id = id;
friends = new HashSet<>();
degree = 0;
}
}
我们可以用代码随机生成用户间的关系。首先根据指定的用户数量,生成Node[]数组,以及数组中的每个用户的节点Node。然后根据边的数量,生成用户之间的相识关系。需要注意的是,自己不能是自己的好友,而且某个用户的所有好友之中不能有重复的人。
Node[] user_nodes = new Node[user_num];
// 生成所有表示用户的结点
for (int i = 0; i < user_num; i++) {
user_nodes[i] = new Node(i);
}
// 生成所有表示好友关系的边
for (int i = 0; i < relation_num; i++) {
int friend_a_id = rand.nextInt(user_num);
int friend_b_id = rand.nextInt(user_num);
if (friend_a_id == friend_b_id) continue;
// 自己不能是自己的好友。如果生成的两个好友id相同,跳过
Node friend_a = user_nodes[friend_a_id];
Node friend_b = user_nodes[friend_b_id];
friend_a.friends.add(friend_b_id);
friend_b.friends.add(friend_a_id);
}
其中,user_num-用户的数量,也就是结点的数量。relation_num-好友关系的数量,也就是边的数量。由于HashSet有去重的功能,所以我这里做了简化处理,没有判断是否存在重复的边,也没有因为重复的边而重新生成另一条边。
随后我们的主角,广度优先搜索就要出场了。这里我使用了一个visited变量,存放已经被访问过的结点,防止回路的产生。
/**
* @Description: 通过广度优先搜索,查找好友
* @param user_nodes-用户的结点;user_id-给定的用户ID,我们要为这个用户查找好友
* @return void
*/
public static void bfs(Node[] user_nodes, int user_id) {
if (user_id > user_nodes.length) return; // 防止数组越界的异常
Queue<Integer> queue = new LinkedList<Integer>(); // 用于广度优先搜索的队列
queue.offer(user_id); // 放入初始结点
HashSet<Integer> visited = new HashSet<>(); // 存放已经被访问过的结点,防止回路
visited.add(user_id);
while (!queue.isEmpty()) {
int current_user_id = queue.poll(); // 拿出队列头部的第一个结点
if (user_nodes[current_user_id] == null) continue;
// 遍历刚刚拿出的这个结点的所有直接连接结点,并加入队列尾部
for (int friend_id : user_nodes[current_user_id].friends) {
if (user_nodes[friend_id] == null) continue;
if (visited.contains(friend_id)) continue;
queue.offer(friend_id);
visited.add(friend_id); // 记录已经访问过的结点
user_nodes[friend_id].degree = user_nodes[current_user_id].degree + 1; // 好友度数是当前结点的好友度数再加1
System.out.println(String.format("\t%d度好友:%d", user_nodes[friend_id].degree, friend_id));
}
}
}
需要注意的是,这里用户结点之间的边是随机生成的,所以每次结果会有所不同。如果想重现固定的结果,可以从某个文件加载用户之间的关系。
小结
在遍历树或者图的时候,如果使用深度优先的策略,被发现的结点数量可能呈指数级增长。如果我们更关心的是最近的相连结点,比如社交关系中的二度好友,那么这种情况下,广度优先策略更高效。也正是由于这种特性,我们不能再使用递归编程或者栈的数据结构来实现广度优先,而是需要用到具有先进先出特点的队列。

思考题
在计算机的操作系统中,我们常常需要查看某个目录下的文件或子目录。现在给定一个目录的路径,请分别使用深度优先和广度优先搜索,列出该目录下所有的文件和子目录。对于子目录,需要进一步展示其下的文件和子目录,直到没有更多的子目录。
欢迎在留言区交作业,并写下你今天的学习笔记。你可以点击“请朋友读”,把今天的内容分享给你的好友,和他一起精进。

精选留言
#include <dirent.h>
#include <stdlib.h>
#include <string.h>
#include <unistd.h>
#include <iostream>
#include <regex>
#include <stack>
using namespace std;
class FileSearch {
private:
stack<string> path; // 路径栈
public:
/**
* Detail: DFS显示ubuntu指定目录下文件
* basePath- 文件路径
* return: null
*/
void DfsFile(char *basePath) {
DIR *dir;
struct dirent *ptr;
char base[1000];
char temp[1000];
// 路径入栈
path.push(basePath);
// 遍历开始
while (!path.empty()) {
// 打开当前目录
strcpy(temp, path.top().c_str());
path.pop();
cout << "Current path: " << temp << endl;
if ((dir = opendir(temp)) == NULL) {
perror("Open dir error, please input the right path");
exit(1);
}
// 显示当前路径下的文件
while ((ptr = readdir(dir)) != NULL) {
// 忽略隐藏文件和路径: .and..
if (regex_match(ptr->d_name, regex("\\.(.*)"))) {
continue;
}
if (ptr->d_type == 8) {
// A regular file
//cout << "file: " << basePath << "/" << ptr->d_name << endl;
cout << ptr->d_name << endl;
} else if (ptr->d_type == 4) {
// 检测为文件夹
memset(base, '\0', sizeof(base));
strcpy(base, temp);
strcat(base, "/");
strcat(base, ptr->d_name);
path.push(base);
continue;
}
}
}
// 关闭文件
closedir(dir);
}
};
int main(void) {
FileSearch test;
// 需要遍历的文件夹目录
char basePath[] = {"/home/joe/Desktop/leetcode"};
test.DfsFile(basePath);
return 0;
}
// 大致输出结果为:
Current path: /home/joe/Desktop/leetcode
leetcodePractice.cpp
a.out
README.md
Current path: /home/joe/Desktop/leetcode/math_fundamental_algorithms
recursion.cpp
tree_depth_first_search.cpp
recursion_integer.cpp
permutation.cpp
dynamic_programming.md
iteration_way.cpp
tree_breadth_first_search.md
a.out
tree_breadth_first_search.cpp
math_induction.cpp
byte_operation.cpp
......
我这边visited集合没有把user_id加入,导致的问题。
控制台的输出日志。我查询的是user_id是 0, 而控制台打印了一行记录是 2度好友:0 。 出现这个打印的原因是遍历0的好友。该好友的friends包含了0,在for循环中算了user_id=0的情况。
谢谢老师指正!
1. 防止数组越界的异常,user_id 等于数组长度也会越界。
2.遍历子节点的时候,如果子节点friends中存在需要查询的user_id,则出现错误的打印输出。如果是查询的user_id应该continue。
控制台打印
0:[3]:0
1:[3]:0
2:[3]:0
3:[0, 1, 2, 4]:0
4:[3]:0
1 度好友:3
2 度好友:0
2 度好友:1
2 度好友:2
2 度好友:4
代码如下,
public static Node[] init(int user_num, int relation_num) {
Random rand = new Random();
Node[] user_nodes = new Node[user_num];
// 生成所有表示用户的节点
for (int i = 0; i < user_num; i++) {
user_nodes[i] = new Node(i);
}
// 生成所有表示好友关系的边
for (int i = 0; i < relation_num; i++) {
int friend_a_id = rand.nextInt(user_num);
int friend_b_id = rand.nextInt(user_num);
if (friend_a_id == friend_b_id)
continue;
Node friend_a = user_nodes[friend_a_id];
Node friend_b = user_nodes[friend_b_id];
friend_a.friends.add(friend_b_id);
friend_b.friends.add(friend_a_id);
}
return user_nodes;
}
public static void bfs(Node[] user_nodes, int user_id) {
// 防止数组越界异常
if (user_id >= user_nodes.length)
return;
// 用于广度优先搜索的队列
Queue<Integer> queue = new LinkedList<>();
// 放入初始节点
queue.offer(user_id);
// 存放已经被访问过的节点,防止回路
HashSet<Integer> visited = new HashSet<>();
while (!queue.isEmpty()) {
// 取出队列头部的第一个节点
int current_user_id = queue.poll();
if (user_nodes[current_user_id] == null)
continue;
// 遍历刚刚拿到的这个节点的所有直接连接节点,并加入队列尾部
for (int friend_id : user_nodes[current_user_id].friends) {
if (user_nodes[current_user_id] == null)
continue;
if (visited.contains(friend_id))
continue;
queue.offer(friend_id);
// 记录已经访问过的节点
visited.add(friend_id);
// 好友度数是当前节点的好友度数再加1
user_nodes[friend_id].degree = user_nodes[current_user_id].degree + 1;
System.out.println(String.format("\t%d 度好友:%d", user_nodes[friend_id].degree, friend_id));
}
}
}
public static void main(String[] args) {
Node[] user_nodes = init(5, 8);
for (Node d : user_nodes) {
System.out.println(d.user_id + ":" + d.friends + ":" + d.degree);
}
bfs(user_nodes, 0);
}
namespace FilePathOperator {
struct St_FilePathNode;
typedef std::set<St_FilePathNode*> SetterFilePathNode;
typedef void(*FilPathOperator)(const St_FilePathNode& rStFilePathNode);
typedef struct St_FilePathNode {
int m_nLevel;
std::string m_strFilePath;
SetterFilePathNode m_setChildernPathNodes;
}StFilePathNode;
};
void FilePathOperator::BFSFilePathNodes(StFilePathNode * pRoot, FilPathOperator nodeOperator, int nMaxLevel)
{
if (NULL == pRoot)
return;
std::deque<StFilePathNode*> queNode;
queNode.push_front(pRoot);
pRoot->m_nLevel = 0; // Root Level is first one
while (!queNode.empty())
{
StFilePathNode* pNode = queNode.back();
queNode.pop_back();
if (NULL == pNode) continue;
int nNodeLevel = pNode->m_nLevel;
nodeOperator(*pNode);
if (nNodeLevel + 1 > nMaxLevel) continue; // childern beyond MaxLevel
SetterFilePathNode::iterator ChildItr = pNode->m_setChildernPathNodes.begin();
for (; ChildItr != pNode->m_setChildernPathNodes.end(); ChildItr++) {
if (NULL == *ChildItr)
continue;
(*ChildItr)->m_nLevel = nNodeLevel + 1;
queNode.push_front(*ChildItr);
}
}
}
void FilePathOperator::DFSFilePathNodes(StFilePathNode * pRoot, FilPathOperator nodeOperator, int nMaxLevel)
{
if (NULL == pRoot)
return;
std::deque<StFilePathNode*> deqNode;
deqNode.push_front(pRoot);
pRoot->m_nLevel = 0; // Root Level is first one
while (!deqNode.empty())
{
StFilePathNode* pNode = deqNode.front();
deqNode.pop_front();
if (NULL == pNode) continue;
int nNodeLevel = pNode->m_nLevel;
nodeOperator(*pNode);
if (nNodeLevel + 1 > nMaxLevel) continue; // childern beyond MaxLevel
SetterFilePathNode::iterator ChildItr = pNode->m_setChildernPathNodes.cbegin();
for (; ChildItr != pNode->m_setChildernPathNodes.cend(); ChildItr++) {
if (NULL == *ChildItr)
continue;
(*ChildItr)->m_nLevel = nNodeLevel + 1;
deqNode.push_front(*ChildItr);
}
}
}
(其他的Create、Destroy、Print就暂时不贴出来了)
class Node:
def __init__(self, number):
self.num = number
self.nodes = []
def setNode(self, num):
if(self.nodes.__contains__(num) == False):
node = Node(num)
self.nodes.append(node)
return node
else:
return None
def setNodeUnder(self, num, base):
if (self.num == num):
return self.setNode(num)
baseNode = self.get(base, self.nodes)
if baseNode == None:
return None
else:
return baseNode.setNode(num)
def get(self, num, nodes=None):
if(self.nodes == None or len(nodes) == 0):
return None
else:
someNodes = []
for node in nodes:
if node.num == num:
return node
for n in node.nodes:
someNodes.append(n)
return self.get(num, someNodes)
def search(self):
print(self.num)
self.printNodes(self.nodes)
def printNodes(self, nodes=None):
if nodes == None or len(nodes) == 0:
return
else:
someNodes = []
for node in nodes:
print(node.num)
for n in node.nodes:
someNodes.append(n)
return self.printNodes(someNodes)
root = Node(110)
root.setNode(123)
root.setNode(879)
root.setNode(945)
root.setNode(131)
root.setNodeUnder(162, 123)
root.setNodeUnder(587, 123)
root.setNodeUnder(580, 945)
root.setNodeUnder(762, 945)
root.setNodeUnder(906, 131)
root.setNodeUnder(681, 587)
root.search()
output:
110
123
879
945
131
162
587
580
762
906
681
finish...